Таким образом получен один из вариантов решения. Если иметь в виду, что коэффициенты приоритетности в достижении целей можно менять с некоторым шагом и в некоторых диапазонах, а также изменять ограничения на повышение или снижение показателей нижнего уровня, то можно получить огромное количество вариантов, которые и являются основой для построения матрицы решений.
Выбор решения осуществляется согласно выработанному с помощью первой процедуры критерию.
Наполнение системы данными и знаниями. Данная процедура предусматривает отчуждение субъективных знаний у ЛПР для настройки СППР. Системе следует сообщить:
· приоритетность в достижении цели на различных уровнях дерева, а также шаг и диапазон изменения коэффициентов относительной важности (КОВ);
· ограничение на используемые ресурсы, а также диапазон их изменения;
· критерий, согласно которому следует выбирать вариант решения;
· форму выдаваемой информации для ЛПР (таблица, диаграмма, график и т.д.).
Исходные данные из бухгалтерской, финансовой и другой отчетности, а также информация из внешних источников (ставки рефинансирования, кредитные ставки, таможенные пошлины и т.д.) поступают из базы данных.
Анализ предложенного варианта решения. СППР может лишь предложить вариант (варианты) решения, но не может его принять. Ответственность за принятие решения несет ЛПР, поэтому оно должно взвесить все возможные последствия данного шага. Если у него возникают какие-либо сомнения, либо появились новые соображения, которые можно ввести в систему и получить уточненное решение, то СППР повторно выполняет необходимые расчеты и предоставляет новый вариант решения.
В основном это касается функционирования СППР на среднем уровне управления. Системы же, применяемые на высшем уровне, используют еще в большой мере информацию из окружающей среды, которая отличается от внутренней еще большей неточностью, недостоверностью, приблизительностью, противоречивостью. Как правило, применение деревьев целей здесь затруднительно, ибо ни цели, ни пути их достижения не ясны. Поэтому СППР, обслуживающие высший уровень управления, используют обычно базы знаний в форме деревьев вывода (деревья И-ИЛИ).
Рассмотрим, каким образом представляются знания в базе знаний с помощью деревьев вывода. Основу их создания составляют правила типа ЕСЛИ-ТО. Например ЕСЛИ А, ТО В. Графически оно представится так:
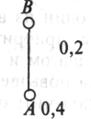
Здесь А — это условие, В — заключение. Далее условимся заключение, получаемое с помощью правила, изображать сверху, а условия — снизу. Число рядом с условием указывает на его достоверность (определенность), а число рядом с линией — на определенность самого правила. Коэффициент определенности колеблется от -1 до 1. Значение -1 указывает на полную неопределенность, а 1 — на полную определенность.
Условий в правиле может быть несколько; они связаны между собой связками И или ИЛИ. Например,
ЕСЛИ А и В и С, ТО Е,
ЕСЛИ А или В или С, ТО Е.
Графически эти правила представляются так:
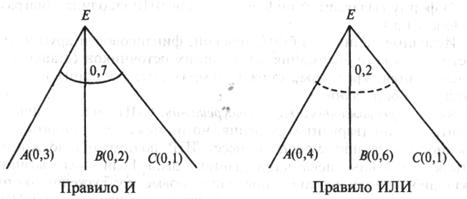
Число, указанное рядом с дугой (сплошной или пунктирной), указывает на определенность правила, а числа рядом с условиями — на определенность условия.
Лицо, принимающее решение, присваивает условиям (А, В, С) и правилу некоторый коэффициент определенности от -1 до 1. С помощью специальных формул рассчитывается коэффициент определенности для заключения.
Для простого правила, содержащего лишь одно условие, например, ЕСЛИ Е ТО С, коэффициент определенности для заключения С рассчитывается так:
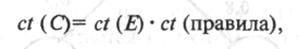
где ct (С) — коэффициент определенности заключения С;
ct (Е) — коэффициент определенности условия Е;
ct (правила) — коэффициент определенности правила.
Пример:
При ct (E)=0,4l
ct (правила) =0,2 коэффициент определенности заключения равен ct (C)=0,08.
Если в правиле несколько условий, связанных связкой И, то для определения коэффициента достоверности заключения применяется следующая операция:
ЕСЛИ (E1 и Е2), ТО С
ct (El и Е2) = min (ct (El), ct (E2)).
Для правила, в котором присутствуют несколько условий, связанных связкой ИЛИ, применяется операция вида:
ЕСЛИ (El или Е2), ТО С
ct (El или El) = max (ct (El), ct (El)).
Пример:
ЕСЛИ (El и E2), TO С ct (El)=0,7;
ct (Е2)=0,6;
ct (правила)=0,8;
ct (условия)= min (0,7;0,6)=0,6;
ct(С)=0,6 * 0,8=0,48.
Если одно и то же заключение поддерживается несколькими правилами, то используется следующая операция:
ЕСЛИ El, TO С ЕСЛИ Е2, ТО С
ct (С)= ct (E1)+ ct (Е2) - ct (El) * ct (E2).
Пример:
ct (Е1)= 0,5;
ct (E2)= 0,4;
Тогда ct(С)=0,7.
Рассмотрим дерево вывода, содержащее несколько правил для определения коэффициента достоверности некоторой гипотезы. Обратимся к рис.5.9, где представлено дерево вывода, содержащее пять правил.
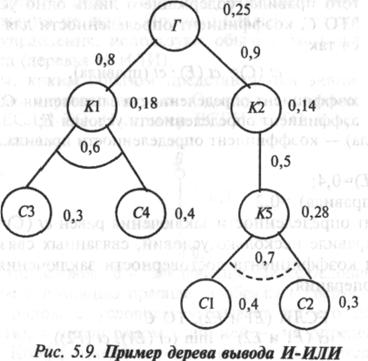
Рядом с узлами дерева указаны коэффициенты определенности 1 условий, а рядом с дугами — правил. Расчет всегда начинается снизу, поэтому вначале выясним, чему равен коэффициент определенности для заключения A3.
ct (К5)= ct (условия) • ct (правила);
ct (условия)= max (ct (Cl), ct (C2))= 0,4;
ct (К5)=0,28.
Для заключения К2 этот коэффициент равен:
ct(K2)=0,5 -0,28=0,14.
Для заключения К1 соответственно:
ct (K1)= ct (условия) * ct (правила);
ct (условия)=min (ct (СЗ), ct (C4)) = 0,3;
ct(К1)=0,18.
Коэффициент достоверности для гипотезы Г выводится на основании двух независимых правил. Вначале он рассчитывается поочередно, исходя из каждого правила:
сt (K1-Г)= 0,8-0,18= 0,14;
сt(K2-1)=0,9-0,14=0,12.
Окончательная оценка гипотезы следующая:
ct (Г)=0,14+0,12 - 0,14 • 0,12=0,25.
В качестве условий в правилах часто используются реляционные 1 выражения, содержащие арифметические (+, -, *, /) или логические 1 (=, <, >) операции.
Реляционные выражения используются в качестве индикаторов, реагирующих на информацию из базы данных. Если из базы данных поступила информация, которая подтверждает истинность реляционного выражения, то знак, находящийся рядом с коэффициентом достоверности условия, остается прежним. В противном случае знак меняется на противоположный.
Показатели, используемые в реляционных выражениях, могут либо прямо поставляться из базы данных, либо предварительно рассчитываться по определенным формулам. На рис. 5.10 показана информационная поддержка расчетов, состоящая как из прямых поставок значений показателей из базы данных, так и предварительно рассчитанных.
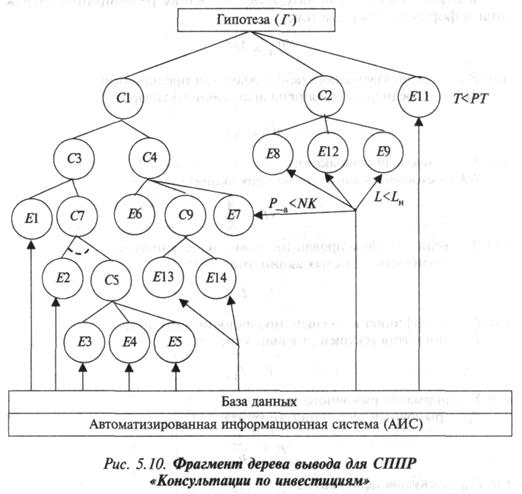
Рассмотрим процесс функционирования СППР на примере принятия решения в области инвестиций. Допустим, перед руководством предприятия возникла проблема принятия решения на вложение средств в акции другого предприятия. Целесообразность инвестирования средств в акции конкретного эмитента, осуществляющего эмиссию ценных бумаг, оценивается с помощью следующих показателей:
· реальная отдача от инвестиций должна быть не ниже средней отдачи в экономике;
· ожидаемый риск должен быть ниже.
Сформулируем гипотезу следующим образом: акции данного предприятия являются перспективными.
Задача состоит в расчете коэффициента достоверности данной гипотезы от -1 до 1. Фрагмент дерева вывода, представленный на рис. 5.10, содержит девятнадцать правил. Правила находятся в табл. 5.1, а расшифровка условий и заключений — в табл. 5.2.
В дереве вывода используются следующие реляционные выражения и формулы для расчетов:
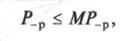
где Р-р — средневзвешенная цена продукции предприятия; МР-р — среднерыночная цена аналогичного товара;

